在现代科技发达的时代,计算机已经成为人们生活中不可或缺的工具之一。然而,尽管计算机在执行数学运算时表现出色,但在某些情况下,电脑数值减法也可能出现错误。本文将探讨电脑数值减法中常见的错误,以及解决这些错误的方法。

精度误差导致计算结果不准确
由于计算机内部使用二进制进行数值计算,而不是我们通常使用的十进制,这就导致了精度误差。这种误差可能在一系列的数值计算过程中累积,并最终导致计算结果与实际结果不完全一致。
舍入误差引发计算结果偏差
在计算机内部,数字通常以有限的二进制位数表示。当计算机需要对一个较大的数值进行减法运算时,可能会导致舍入误差,从而引发计算结果的偏差。这是由于计算机只能存储一定数量的有效数字。
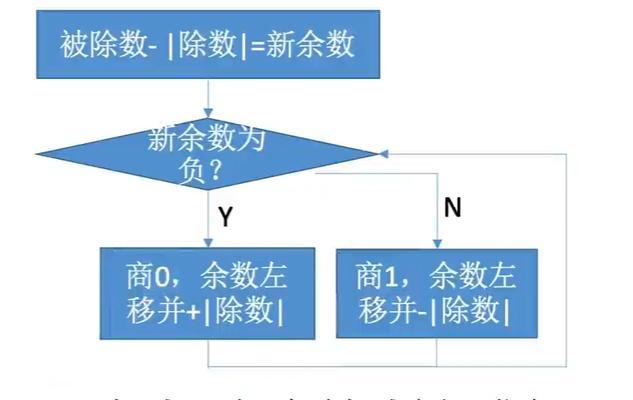
计算机减法中的数值溢出问题
当计算机进行减法运算时,如果结果超出了它所能表示的范围,就会发生数值溢出。这种情况下,计算机将无法给出正确的结果,并可能产生错误的输出。
浮点数运算中的舍入误差
浮点数是计算机中用于表示实数的一种数据类型。然而,浮点数在计算中往往会出现舍入误差,导致计算结果的不准确。这主要是由于浮点数的精度有限,并且无法表示所有的实数。
无限循环小数的处理问题
在某些情况下,减法运算可能会产生无限循环小数。然而,由于计算机内部对小数的存储方式是有限位数的,这就导致了无限循环小数的截断。在这种情况下,计算结果也将产生偏差。

采用高精度计算方法解决精度误差
为了解决精度误差问题,可以采用高精度计算方法,如使用更多位数的二进制表示数字,或者使用十进制计算方法来执行减法运算。这样可以提高计算结果的准确性。
精确控制舍入误差的方法
为了避免舍入误差引发的偏差,可以采用四舍五入、向上取整或向下取整等方法,精确控制计算结果的舍入方式。这样可以尽可能减小舍入误差对计算结果的影响。
采用溢出判断机制解决数值溢出问题
为了解决数值溢出问题,可以引入溢出判断机制,在进行减法运算之前先判断结果是否超出了计算机所能表示的范围。这样可以及时发现并处理溢出情况,避免错误的输出。
使用更高精度的浮点数表示
为了解决浮点数运算中的舍入误差问题,可以使用更高精度的浮点数表示,如使用双精度浮点数(double)代替单精度浮点数(float)。这样可以提高计算结果的准确性。
采用有效的截断策略处理无限循环小数
对于产生无限循环小数的减法运算,可以采用有效的截断策略来处理。例如,可以将计算结果截断到一定位数,或者使用循环标记来表示无限循环小数。
优化算法以提高计算准确性
除了使用更高精度的数据表示方法,还可以优化减法运算的算法,以提高计算准确性。例如,可以通过改变计算顺序、引入中间结果的缓存等方式来减小计算误差。
增加计算过程的容错性
为了应对可能发生的错误,可以增加计算过程的容错性。例如,在进行减法运算时,可以检查输入数据是否有效,并及时处理可能出现的错误情况。
引入数值校验机制以确保结果准确
为了确保计算结果的准确性,可以引入数值校验机制。这可以通过与已知正确结果进行比较,或者使用数值校验算法来判断计算结果是否符合预期。
持续优化和改进数值减法算法
随着科技的不断进步,数值减法算法也将不断改进和优化。人们可以通过研究新的数值计算方法、改进硬件设备等方式,不断提高电脑数值减法的准确性和效率。
电脑数值减法在实际应用中可能出现各种错误,如精度误差、舍入误差、数值溢出等。然而,通过采用高精度计算方法、精确控制舍入误差、引入溢出判断机制等措施,可以有效解决这些问题,提高电脑数值减法的准确性和可靠性。